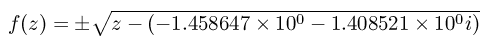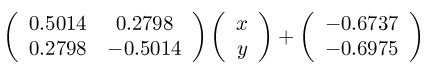|
The images you see to the right were all created with IFS Linear.* 
Click any image to see a larger view. Click here or click the logo above for a test drive! IFS Linear is free
software. Download it at Sourceforge! * The basic shapes were created with IFS Linear. The 3-d effects were added with the GIMP. Click here to learn more about processing IFS Linear images with the GIMP. |
 koch.lifs |
|
 horns.lifs |
 spiral.lifs |
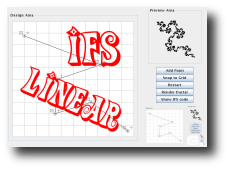
IFS Linear is a program for creating cool graphics like the ones you see above. Though you don't need to know it in order to use the program, the cool graphics it produces are actually iterated function system (IFS) fractals. That's where it gets the "IFS" part of its name.
When the applet starts up, you should see a gridded design area. That grid is where you will design your fractal. No time like the present to experiment a little. Click the "Add Point" button. You should see a circle tool appear in the center of the design area. Click and drag the circle out of the center. Then click the "Add Point" button again. Drag the new circle out of the center as well, and click the "Add Point" button a third time. Now you have enough circles in order to make a fractal. There may or may not be anything showing in the preview area at this point. It depends on whether the distance between the first and last points is greater than the lengths of all the line segments or not (as illustrated below).
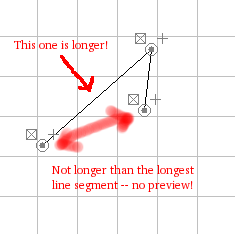
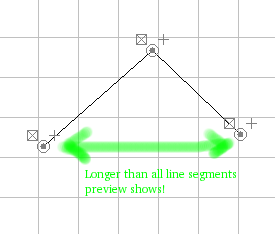
If you do not see a fractal in the preview area, drag one of the endpoints around until you do. You may also add a fourth point or even more points. But no matter how many points you have, the distance between the first and last has to be greater than the length of every line segment. This table summarizes what you can do with circle tools.
 |
Translate
Tool Use this tool to move the circle. |
 |
Flip
Sides Tool The copy given by a line segment is flipped across the segment. |
 |
Reverse
Direction Tool The copy given by a line segment is toggled between forward and backward. |
 |
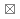Delete
Tool Use this tool to delete the circle. |
Clicking the "Restart" button erases all circle tools. It's sort of a "start over" button.
Clicking "Snap to Grid" makes circle tools "snap" from one location to another as you drag them around. With "snap" on, the circle tools can only be placed in limited locations. This is useful if you want to place circles exactly on grid crossings or half-way points. Notice that when you click the button, it turns into a "Freehand" button. Clicking the "Freehand" button removes "snapping."
When you like what you see in the preview area, you might want to click on the "Render Fractal" button. This will bring up a dialog box that allows you to create a larger, more colorful version of your fractal! Horns was rendered using the Random method; Lightning was rendered with the single color method; Spiral was rendered with the one color per map method; and Koch was rendered with the deterministic method. Feel free to try them all, but be careful with the deterministic method. It's not a mistake that the number of iterations is small. It takes a long time to do each iteration, and not very many are needed to create interesting renderings.
You can make the Classic Koch curve several different ways. Two of them are shown below.
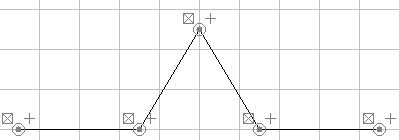
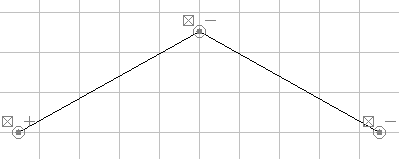
Notice the minus signs in the second one! Actually, neither one of these is exactly the Koch curve because the peak is just slightly off in each one. But it's the best you can do with "snap" on. With snap off, you can get a little closer, but still never hit it exactly since the peak would need to be located at a point with an irrational y-coordinate. That's never going to happen!
As stated before, the first and last points must be a distance away from one another that is greater than the length of any line segment you see! This is easiest is you spread the first and last points as far from one another as you can for the given shape you are trying to create.
The .lifs
files hold
the mathematical description of your IFS fractal! It may or may not
interest you, but this is how IFS Freestyle sees the shapes in the
design area. Also, if you download the stand-alone
version, you will get save and open buttons so you can save
and retrieve your work. The .lifs
file is what is saved and read during these operations. A line like
Julia:-1.458647e+00,-1.408521e+00,false
is the mathematical description for the complex number mapping
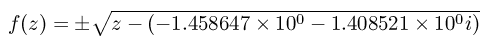
where the plus or minus is chosen according to whether or not the last parameter is "true" or "false." True means positive and false means negative.
However, Linear IFS just uses this information to save the locations of the points and whether they are positive or negative. It does not use this interpretation at all (IFS Julia does)! Click "Show IFS Code" to see the actual IFS Code. You will see lines like this:
AffineMap:( 0.5014 , 0.2798 , 0.2798 , -0.5014 , -0.6737 , -0.6975 )
This stands for the transformation
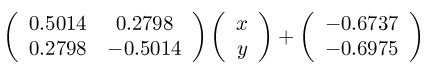
Each one of these transformations is a similitude that maps the baseline (the imaginary line segment connecting the first and last points) to one of the line segments in your generator.
