IFS
Freestyle
What is IFS Freestyle?
IFS Freestyle is a program for creating cool graphics like the ones you
see above. Though you don't need to know it in order to use
the program, the cool graphics it produces are actually iterated
function system (IFS) fractals. That's where it gets the
"IFS" part of its name.
How do you use IFS
Freestyle?
- Basic Usage
- Affine transformations
- Julia transformations
- Rendering
- Tips and Tricks
- Julia Sets
- Mix and match
- Coverage
- How to make a fern
1. Basic usage
a. Affine
transformations
Add an affine transformation to the design area by clicking
the "Add Affine Transformation" button. You will see a highly
decorated square appear. Your cool graphics are created by
massaging at least two of these squares, but let's work with the one we
have for now.
The decorations are actually tools for doing the massaging.
After certain massages, the square may no longer be a square, so the
following table refers to it as a quadrilateral. Don't be afraid of the
long list of tools, or their definitions. Just grab one with
your mouse, and drag to see what happens. Now is a good time to
experiment a little. Massage your square with some of these tools. Even
if you don't experiment with all the tools right now, make sure you DO
use the translate tool to move the square so it's not right in the
middle of the design area.
 |
Rotate
Tool
Use this tool to spin the quadrilateral. |
 |
Translate
Tool
Use this tool to move the quadrilateral. |
 |
Reflect
Tool
Use this tool to make a mirror image of the
quadrilateral. |
 |
Scale Tool
Use this tool to change the size of the
quadrilateral. |
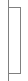 |
 |
More
Scale Tools
Use these tools to change the size of the quadrilateral in one
direction, but not the other. |
 |
 |
Shear
Tools
Use these tools to turn the square into a diamond
shape. |
 |
Delete
Tool
Use this tool to delete the quadrilateral. |
Add a second quadrilateral by clicking the "Add Affine
Transformation" button again. As soon as the second transformation
appears, an image should show in the preview area. This shows you the
shape you have created so far. At this point, it's probably not too
exciting, but just wait! Massage this quadrilateral and watch the
preview change as you massage the new quadrilateral. Add a third, and
perhaps a fourth, and see what you can come up with!
b. Julia
Transformations
If you have any transformations in the design area, delete
them with their delete tools  . Now
click the "Add Julia Transformation" button. You will see a circular
tool with a couple of decorations. Just as with the affine
transformations, your cool graphics are created by massaging at least
two of these circles. Here is what the tools do.
. Now
click the "Add Julia Transformation" button. You will see a circular
tool with a couple of decorations. Just as with the affine
transformations, your cool graphics are created by massaging at least
two of these circles. Here is what the tools do.
 |
Translate
Tool
Use this tool to move the circle. |
 |
Plus/Minus
Toggle
Use this tool to toggle the sign of this tool. |
 |
Delete
Tool
Use this tool to delete the circle. |
Now is a good time to experiment a little. Massage your circle
with one or both of the translate and plus/minus tools. Notice nothing
happens in the preview area. Nothing will happen until you
add a second transformation. Do it by clicking the "Add Julia
Transformation" button again. Massage this circle and watch
the preview change as you move it around.
c. Rendering
When you like what you see in the preview area, you might want
to
click on the "Render Fractal" button. This will bring up a dialog box
that allows you to create a larger, more colorful version of your
fractal! Curly was rendered using the Random method; the fern was
rendered with the single color method; the sierpinski triangle was
rendered with the one color per map method; and the tile was rendered
with the deterministic method. Feel free to try them all, but be
careful with the deterministic method. It's not a mistake that the
number of iterations is small. It takes a long time to do each
iteration, and not very many are needed to create interesting
renderings.
2. Tips and Tricks
a. Julia Sets
You can make classic Julia Sets by making one of the circles positive
and the other negative, and placing them right on top of one
another. That's where the transformation gets its name.
b. Mix and match
Even though the basic usage examples had you using
only one or the
other type of transformation, you can use both kinds at the same time!
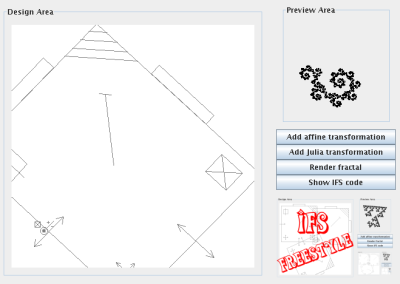
Here is a screenshot of the making of the curly graphic above. Notice
the Julia transformation near the bottom left corner of the design area.
c. Coverage
As in the example above,
the best
graphics are made when a lot, but not all of the design area is covered
by transformations. NOTE: This does not apply when you are using only
Julia transformations. Also, not to worry if the transformations fall a
little outside of the design area.
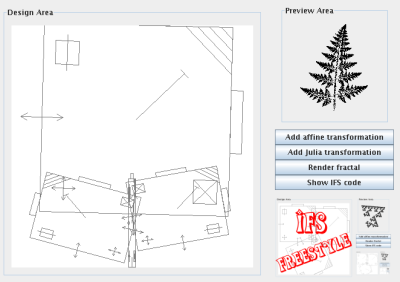
d. How to make the fern
The fern is made with 4 affine transformations placed like so
in the
design area. Notice that the one in the bottom right has been
reflected. The others have not. The fern was rendered in the single
color green.
What are .fifs files?
The .fifs
files hold
the mathematical description of your IFS fractal! It may or may not
interest you, but this is how IFS Freestyle sees the shapes in the
design area. Also, if you download the stand-alone
version, you will get save and open buttons so you can save
and retrieve your work. The .fifs
file is what is saved and read during these operations. A line like
AffineBasics:7.624844e-01,9.264101e-01,8.226161e-02,-1.102754e-01,9.074441e-01,-3.107769e-01,-3.208020e-01,false
is the mathematical description for an affine transformation
with
| horizontal scaling |
7.624844 x 10-1 |
| vertical scaling |
9.264101 x 10-1 |
| horizontal shearing (in radians) |
8.226161 x 10-2 |
| vertical shearing (in radians) |
-1.102754 x 10-1 |
| rotation (in radians) |
9.074441 x 10-1 |
| reflected |
false |
| horizontal translation |
-3.107769 x 10-1 |
| vertical translation |
-3.208020 x 10-1 |
applied in that order. A line like
Julia:-1.458647e+00,-1.408521e+00,false
is the mathematical description for the complex number mapping
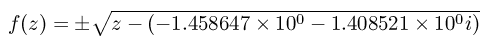
where the plus or minus is
chosen
according to whether or not the last parameter is "true" or "false."
True means positive and false means negative. Just click the
"Show
IFS Code" button to see what would be the contents of the .fifs file if
you could save it.
This page is hosted by